Min-Max Correlation Clustering via Neighborhood Similarity
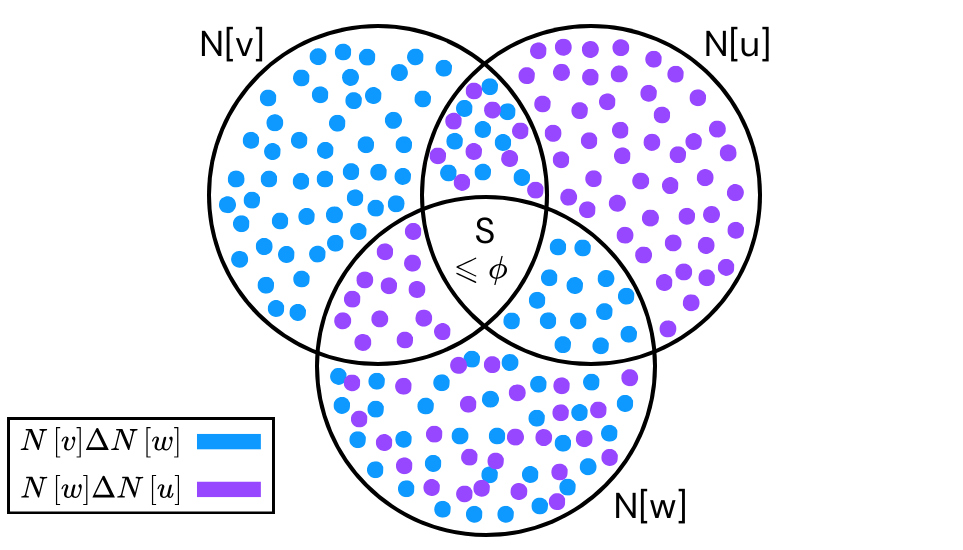
We present an efficient algorithm for the min-max correlation clustering problem. The input is a complete graph where edges are labeled as either positive (+) or negative (−), and the objective is to find a clustering that minimizes the ℓ ∞-norm of the disagreement vector over all vertices. We resolve this problem with an efficient (3+ϵ)-approximation algorithm that runs in nearly linear time, Õ (|E+|), where |E+| denotes the number of positive edges. This improves upon the previous best-known approximation guarantee of 4 by Heidrich, Irmai, and Andres, whose algorithm runs in O(|V|2+|V|D2) time, where |V| is the number of nodes and D is the maximum degree in the graph. Furthermore, we extend our algorithm to the massively parallel computation (MPC) model and the semi-streaming model. In the MPC model, our algorithm runs on machines with memory sublinear in the number of nodes and takes O(1) rounds. In the streaming model, our algorithm requires only Õ (|V|) space, where |V| is the number of vertices in the graph. Our algorithms are purely combinatorial. They are based on a novel structural observation about the optimal min-max instance, which enables the construction of a (3+ϵ)-approximation algorithm using O(|E+|) neighborhood similarity queries. By leveraging random projection, we further show these queries can be computed in nearly linear time.